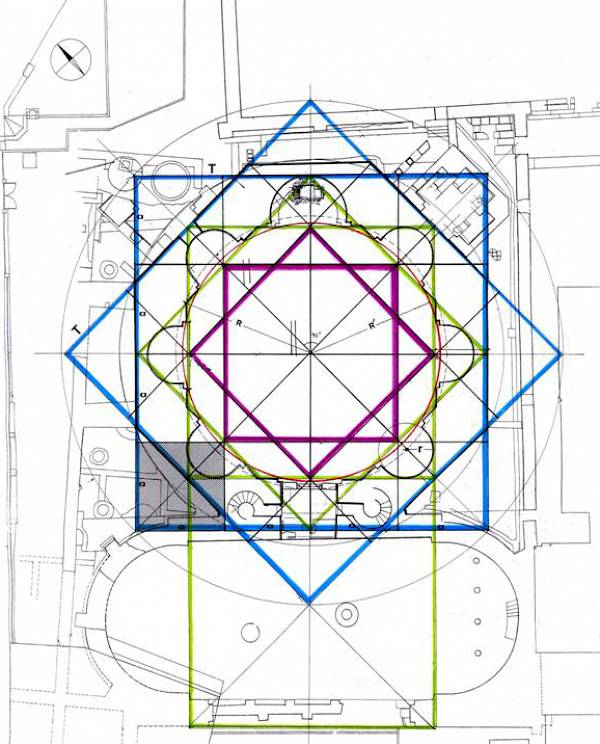
The outer sides (faces) of the Octagon emerged from the intersection of the sides of two equal squares (T), with side (α) equal to 100 feet (32.50 m.) and a diagonal of length a = 141.421 feet (45.96 m.).
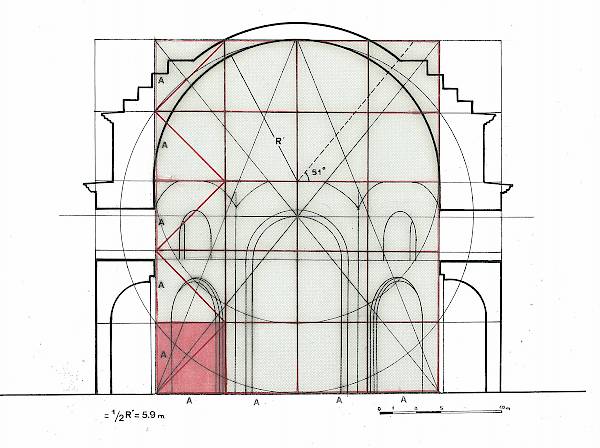
The inner sides of the Octagon, and hence the thickness (γ) of its walls emerged from the intersection of the sides of two equal squares, the corner points of which are in the center of the two initial squares T. In accordance with the above description, the resulting inner octagonal shape is inscribed in a circle with radius R = 12.50 meters (38 feet), on the circumference of which are the centers of the outline χάραξης of the niches, with radius r = 8 feet. The radius r of the niches is associated with the thickness of the walls (γ) with a relationship of (γ) = 2r.
The maximum width of the niches (β) emerged from the intersection of the inner octagon with a circle of radius R', which is equal to approximately ¼ of the diagonal of the original square T. The maximum width (β) of the niches is associated with the radius of the circle in which the inner octagon is inscribed with the relationship: β = 1/2 R = 19π.